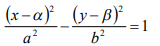Pembelajaran Matematika: 2019

UAS Praktikum Geometri Analitik

Download --> https://drive.google.com/file/d/13sijnZ0TBgbobdHnjduDL_Vt4ZnkKhU_/view?usp=sharing

Geogebra Boloida --> https://drive.google.com/file/d/14WgRk51fqM8GwcpI6FgtKiwwnMddGVr_/view?usp=sharing

Geogebra Elipsoida --> https://drive.google.com/file/d/1PYUw7Yn853jrUFOiIn9J4ZmHinGbaHht/view?usp=sharing

Geogebra Soal --> https://drive.google.com/file/d/1vVdF7eQJ8klIFKMmPjryeF1L1s8zsb7R/view?usp=sharing

Pukul : 16.11 WIB

Persamaan Bola

Assalamualaikum wr.wb
Post kali ini yaitu membahasa singkat tentang Persamaan Bola:

Bola dengan pusat titik O (titik asal) dan berjari-jari r, persamaannya diperoleh dengan cara mengambil sebarang titik P(x, y, z) pada bola. Sehingga

Pada gambar disamping

Karena P(x, y, z) sebarang titik pada bola, maka setiap titik (x, y, z) pada bola berlaku
x^2 + y^2 + z^2 = r^2. Ini berarti persamaan bola dengan pusat O dan berjari-jari r adalah:
x^2 + y^2 + z^2 = r^2.
Selanjutnya akan dicari persamaan bola dengan jari-jari r dan titik pusat M(a, b, c).
Ambil sebarang titik P(x, y, z) pada bola, maka vektor

Karena P(x, y, z) sebarang titik pada bola yamg memenuhi persamaan tersebut diatas, maka setiap titik (x, y, z) pada bola memenuhi persamaan tersebut. Hal ini berarti persamaan bola dengan jari-jari r dan titik pusat (a, b, c) adalah:
(x – a)^2 + (y – b)^2 + (z – c)^2 = r^2.

Contoh :

* Carilah persamaan bola yang berpusat di titik (1, 3, 2) dan melalui titik (2, 5, 0).
Jawab :
Jari-jari bola adalah jarak dua titik tersebut, yaitu :

Persamaan bola yang dicari adalah persamaan bola dengan jari-jari 3 dan berpusat di titik (1, 3, 2), yaitu:

Jika dijabarkan menjadi

Rumus persamaan bola yaitu (x – a)^2 + (y – b)^2 + (z – c)^2 = r^2 dapat ditulis sebagai berikut:

Jika –2a = A, -2b = B, -2c = C, dan a2 + b2 + c2 – r2 = D, maka persamaan bola tersebut dapat ditulis sebagai berikut
x^2 + y^2 + z^2 + Ax + By + Cz + D = 0

Nampak disini bahwa persamaan bola adalah suatu persamaan kuadrat dalam x, y, dan z dengan ciri-ciri:
(a) tidak memuat suku-suku xy, xz, atau yz, dan
(b) koefisien-koefisien x2, y2, dan z2 selalu sama.
Selanjutnya akan ditentukan titik pusat dan jari-jari dari bola dengan persamaan x^2 + y^2 + z^2 + Ax + By + Cz + D = 0.
Persamaan ini bisa diubah dengan melengkapi kuadrat dari x, y, dan z sebagai berikut:

Dari persamaan ini dapat dengan mudah ditentukan titik pusat dan jari-jari bola, yaitu:

Terima Kasih, Semoga Bermanfaat 🙇🙇

Praktikum 7_Kelompok 4_Hiperboloida, Elipsoida dan Paraboloida

DOWNLOAD --> https://drive.google.com/file/d/18TR7B45K82O0MolcAzluGGgl-LmUxtt0/view?usp=sharing

Geogebra video 1 -->https://drive.google.com/file/d/1ncxPCBAr7U5-V3uCmZxPipDSFuPGZp9P/view?usp=sharing

Geogebra Video 2 --> https://drive.google.com/file/d/1XxQO5lYldYzkSpuGriNED40ALVG5qPOJ/view?usp=sharing

Geogebra Video 3 --> https://drive.google.com/file/d/1KTQ1hNWTycRtRe9E8Ai2yboNnlq2v7lA/view?usp=sharing

Praktikum 6 Kelompok 4_ Elips, Parabola dan Hiperbola

DOWNLOAD->https://drive.google.com/file/d/1sypNWdqczmavLgdtGMiGGzSEbQk1aZPM/view?usp=sharing

Hiperbola dan Elips

Assalamualaikum warrahmatullahi wabarakatuh

Pada postingan kali ini saya akan mempost secara ringkas inti - inti hiperbola dan elips

Bangunan - bangunan elips, hiperbola, parabola dan lingkaran ialah bangunan yang terbentuk karena pemotongan dari sebuah bangun kerucut.

Elips

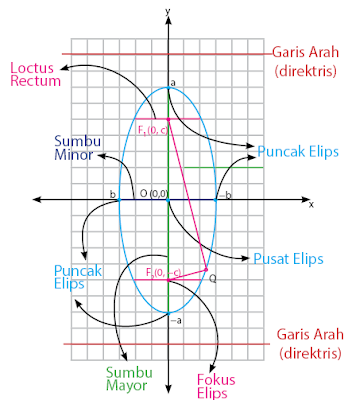
Hasil potongan dari irisan kerucut berikutnya ialah elips. Bentuk elips seperti lingkaran yang dipipihkan. elips dibedakan menjadi dua, yaitu elips horizontal dan elips vertikal. Bagian - bagian elips yang penting untuk dikethui ialah sunbu mayor, sumbu minor, fokus elips, puncak elips, pusat elips, lactus rectum, dsb.

1. Elips Horizontal

Pada elips horizontal ada elips yang terletak pada titik pusat (0,0) dan ada juga yang terletak pada bukan titik pusat atau pada titik (h,k)

seperti gambar berikut

Berdasarkan dua elips di atas, diperoleg persamaan - persamaan di bawah ini

2. Elips Vertikal

sama halnya dengan elips horizontal, elips vertikal juga ada elips yang terletak pada titik pusat (0,0) dan ada juga yang terletak pada bukan titik pusat atau pada titik (h,k)

seperti gambar berikut

dan persamaan yang didapat dari kedua gambar di atas ialah :

Hiperbola

Hiperbola adalah bentuk irisan kerucut yang dipotong secara vertikal. Komponen penysusuk hiperbola ialah kurva, asimtot, garis arah (direktris), titik fokus, titik puncak, dsb. Semua komponen penyusun hiperbola saling berkaitan sehingga dapa dirumuskan sebuah persamaan umum. Nantinya, akan diberikan rumus persamaan hiperbola. Sebelumnya, perhatikan unsur - unsur penyusun hiperbola beikut.

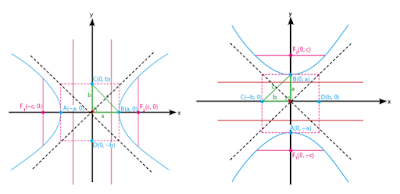
1. Hiperbola horizontal

2. Hiperbola Vertikal

Pada hiperbola yang berpusat pada titik pusat (0,0) terdapat dua buah hiperbola, yaitu hiperbola horizontal dan hiperbola vertikal. seperti berikut :

dan persamaannya didapatkan

Pada hiperbola yang berpusat pada titik pusat (h,k) terdapat dua buah hiperbola, yaitu hiperbola horizontal dan hiperbola vertikal. seperti berikut :

dan persamaannya didapatkan

Sekian dari postingan singkat ini

Semoga bermanfaat 🙇

11.41 WIB

Elips

Assalamualaikum warahmatullahi wabarokatuh

Kembali lagi, setelah sekian lama tidak memposting.
Baiklah pada hari ini saya akan mempost sedikit pengenalan untuk materi elips.

Semoga bermanfaat 🙏🙇

Pada kurva parabola didefinisikan sebagai titik-titik yang rasio (perbandingan) antara jarak dengan titik tetap (fokus) dan jarak dengan garis tetap (garis direktrik) adalah 1. Namun pada elips ini, rasionya kurang dari 1, artinya titik-titik kurva lebih dekat dengan titik fokus dibanding dengan garis direktrik. Elips adalah tempat kedudukan titik-titik yang bergerak dalam bidang sehingga rasio antara jarak dari titik fokus dan jarak dari garis direktrik selalu konstan, yaitu e < 1.

gambar elips diatas yaitu elips yang berpusat pada titik (0,0) yang mana juga berbentuk horizontal, sehingga untuk persamaan elips di atas didapatkan persamaannya yaitu :

> Elips standar jenis kedua adalah elips yang sumbu mayornya sepanjang sumbu y dan sumbu minornya sepanjang sumbu x, seperti pada Gambar. Dengan persamaan kurvanya adalah

dan untuk elips yang umbu mayornya sepanjang sumbu y dan sumbu minornya sepanjang sumbu x, seperti pada Gambar, persamaan elipsnya ialah

Baik elips standar jenis pertama maupun elips standar jenis kedua, bahwa selalu dimisalkan a > b. Sehingga selalu

Jenis kedua elips tak standar yaitu jika sumbu mayornya sejajar dengan sumbu x dan sumbu minornya sejajar dengan sumbu y, lalu titik pusat elips yaitu (h, k), seperti pada gambar dbawah

Persamaan elips untuk jenis ini adalah

Dan jika sumbu mayornya sejajar dengan sumbu y dan sumbu minornya sejajar dengan sumbu x, lalu titik pusat elips yaitu (h, k)

Tugas Hiperbola dan Hiperboloida

Kesimpulan yang didapat dari dua video diatas ialah:

Hiperbola

yaitu suatu kurva yang terbentuk pada bidang dua dimensi, dimana secara definisi hiperbola ialah sebagai tempat kedudukan titik-titik yang bergerak dalam bidang sehingga rasio antara jarak dari titik fokus dan jarak dari garis direktrik selalu konstan, yaitu e > 1.

Persamaan hiperbola yang berpusat pada titik (0,0) ialah

- Fokus F1 (c,0) dan F2(-c,0) dengan c²= a² + b²

- Titik puncak A1 (a,0) dan A2 (-a,0), selisih jarak = 2a dengan c > a

- Persamaan direktris =

$x=\pm\frac{a^{2}}{c}$

persamaan asymtot y =

dan untuk persamaan hiperbola yang berpusat pada a,b

Garis dan Hiperbola Berkemungkinan :

a. Tidak saling memotong, D < 0

b. Momotong di dua titik, D > 0

c. Menyinggung, D = 0

Kurva hiperbola sendiri yaitu hasil perpotongan secara vertikal pada suatu bangun kerucut

2. Hiperboloida

yaitu suatu kurva yang terbentuk pada bidang tiga dimensi, dan secara definisi dapat dikatakan bahwa hiperboloida merupakan himpunan titik-titik di dimensi tiga yang selisih jaraknya terhadap dua titik tetap yang disebut titik fokus adalah sama.