Penyajian Data Kelas 7

Pada materi penyajian data untuk SMP kelas VII, perhatikan video di bawah ini untuk mempelajarinya lebih jelas!

Bangun Datar Kelas 7

Segi Empat 

Segiempat merupakan polygon dengan empat sisi. Segiempat dibedakan menjadi persegi, persegi panjang, belah ketupat, jajargenjang, trapesium, dan layang-layang.  Macam-macam segiempat tersebut diuraikan sebagai berikut

    A. Persegi panjang

                   

1.     Keliling persegi panjang = 2p + 2l

2.         Luas persegi panjang à   p x l

Keliling dan Luas Persegi Panjang

Keliling disimbolkan dengan huruf K sedangkan luas biasa disimbolkan dengan L.

Keliling persegi panjang adalah jumlah semua panjang sisi persegi panjang.

1.      Keliling persegi panjang adalah jumlah semua panjang sisi persegi panjang.

K = Keliling persegi panjang ABCD

K = AB + BC + CD + DA

Karena AB = p , AB = CD, BC = l dan BC = DA maka,

K= p + l + p + l = 2p + 2l = 2 (p + l)

Jadi, rumus untuk mencari keliling persegi panjang adalah :

K = 2p + 2l atau K = 2 (p + l). 

    2. Luas persegi panjang adalah luas daerah yang dibatasi oleh sisi-sisi bangun persegi panjang. Luas persegi panjang dapat dicari dengan menghitung banyaknya persegi satu satuan yang ada pada persegi panjang.

  

Banyaknya persegi = 3

 3 = 3 x 1

Persegi panjang dengan ukuran panjang 3 cm dan ukuran lebar 1 cm memiliki luas 3cm².

Banyaknya persegi = 6

6 = 3 x 2 

Persegi panjang dengan ukuran panjang 3 cm dan ukuran lebar 3 cm memiliki luas 6cm²

Banyaknya persegi = 12

12 = 4 x 3

Jadi, luas persegi panjang dapat dicari dengan mengalikan ukuran panjang dengan lebar persegi panjang. Apabila p adalah panjang dan l adalah lebar, maka L (luas) persegi panjang adalah p x l. Sehingga rumus mencari luas persegi panjang adalah

L = p x l.

 B.    Persegi

Persegi adalah suatu segi empat dengan semua sisinya sama panjang dan semua sudut-sudutnya sama besar dan siku-siku (90⁰ ). Dari pengertian itu diperoleh bahwa setiap sudutnya dibagi dua sama besar oleh diagonalnya dan kedua diagonalnya berpotongan tegak lurus.

a.      Keliling Persegi

Persegi merupakan persegi panjang yang semau sisinya sama panjang sehingga p = l

Karena p = l, maka keliling persegi adalah

k = (2(p + l) = 2(2p) = 2(2l)

misalkan p = l = s, maka K = 4s dengan s = panjang sisi persegi

b.      Luas Persegi

Suatu persegi mempunyai ukuran panjang = lebar atau p = l = s, maka rumus luas persegi adalah L = s x s = s²dengan s = panjang sisi persegi

C. Jajargenjang

Jajargenjang adalah segiempat yang sisisisinya sepasang-sepasang sejajajar, atau segiempat yang memiliki tepat dua pasang sisi yang sejajar.

Berdasarkan proses terbentuknya jajargenjang di muka dapat diperoleh sifat-sifat jajargenjang 

berikut ini.

1. Sisi-sisi yang berhadapan sejajar dan sama panjang, yaitu AB//CD, AD// BC , AB = DC, dan AD = BC

2. Sudut-sudut yang berhadapan sama ukuran, yaitu A = C dan B = D.

3. Dua sudut yang berdekatan saling berpelurus, yaitu A + B = B + C = C + D = D + A =180.

4. Diagonal jajargenjang membagi daerah jajargenjang menjadi dua bagian sama besar, yaitu luas daerah ACB = luas daerah CAD dan luas daerah ADB = luas daerah CBD.

5. Diagonal-diagonalnya saling membagi dua sama panjang, yaitu AO = CO dan BO = DO

a.      Keliling Jajar Genjang

Keliling jajar genjang adalah jumlah panjang keempat sisinya.

Dari Gambar dapat diperoleh keliling jajar genjang ABCD = AB + BC +CD + DA Panjang AB = CD dan AD = BC, maka keliling 

ABCD = 2AB + 2BC + 2(AB + BC). Jadi keliling jajar genjang ABCD adalah: K = 2(AB + BC)

b.      Luas Jajar Genjang

Jajar genjang ABCD terdiri dari dua segitiga yang kongruen, yaitu ABD dan CDB.

Jadi, luas jajar genjang adalah jumlah luas ⃤1 dan ⃤2.

sumber: https://www.kimiamath.com/post/pembuktian-rumus-luas-jajar-genjang

D. BELAH KETUPAT

Belah ketupat adalah segiempat yang semua sisinya sama panjang. Dapat juga dikatakan bahwa: Jika sebuah segiempat kedua diagonalnya saling tegaklurus dan saling membagi dua sama panjang, maka segiempat tersebut adalah belahketupat.

Belah ketupat memenuhi semua sifat jajar genjang, dengan demikian belah ketupat adalah jajar genjang yang kempat sisinya sama panjang, sehingga memiliki sifat-sifat berikut:

1. Setiap sudut dibagi dua sama besar oleh diagonal-diagonalnya,

2. Diagonal-diagonalnya berpotongan saling tegak lurus,

Perhatikan gambar di atas dua segitiga yang kongruen, yaitu ABC dan ABD

a. AC = BC = AD = BD dan AB = AB

b. CAB = DAB = CBA = DBA

c. ADB = ACB

Keliling dan Luas Belah Ketupat

a. Luas daerah belahketupat sama dengan setengah hasil-kali panjang diagonaldiagonalnya.

b. Keliling belahketupat sama dengan empat kali panjang sisinya.

c. Misal L adalah luas daerah belahketupat dengan diagonal-diagonalnya d1 dan d2, maka L = x d1 x d2

Misal K adalah keliling belahketupat dengan panjang sisi s, maka K = 4 x s

E. LAYANG-LAYANG

Segiempat ABCD tersebut dinamakan bangun layanglayang dengan sisi AB , sisi BC , sisi CD , sisi AD , diagonal AC dan BD.

a.      Sifat layang-layang

1.      Panjang dua pasang sisi berdekatan sama, yaitu

AB = AD dan BC = DC. AB @ AD , BC @ DC .

2. Sepasang sudut yang berhadapan sama ukuran, yaitu ukuran

ÐABC = ukuran ADC. ÐABC @ ÐADC

1.      Salah satu diagonalnya membagi layanglayang menjadi dua sama ukuran, yaitu

DABC = DADC atau AC merupakan sumbu simetri.

2.      Diagonal-diagonalnya saling tegak lurus dan salah satu diagonalnya membagi diagonal yang lain menjadi dua sama panjang, yaitu AC ^ BD dan BE =ED.

Berdasarkan sifat-sifat di atas, didefinisikan : Layang-layang adalah segiempat yang diagonal-diagonalnya saling tegaklurus dan salah satu diagonalnya membagi diagonal lainnya menjadi dua sama panjang.

Dengan kata-kata: Luas layang-layang sama dengan setengah Hasil kali diagonal-diagonalnya

Secara simbolik: Misal L adalah luas layanglayang dengan panjang diagonal-diagonalnya d1 dan d2,

maka L = 

     

    F. TRAPESIUM

Trapesium adalah segiempat yang mempunyai tepat sepasang sisi yang berhadapan sejajar. Trapesium

adalah segiempat yang mempunyai tepat sepasang sisi yang berhadapan sejajar. Segiempat ABCD di samping adalah trapesium ABCD. Sisi AB dan DC disebut alas trapesium , sisi AB sejajar dengan sisi DC , sedangkan sisi AD dan sisi BC disebut kaki-kaki trapesium.

Trapesium EFGH di bawah disebut trapesium siku-siku, karena salah satu kaki trapesium tegak lurus dengan alasnya.

Sifat-sifat trapesium, antara lain sebagai berikut.

1. Jumlah ukuran dua sudut yang berdekatan antara dua sisi sejajar pada trapesium adalah 180⁰

(ÐE +ÐH =ÐF +ÐG = 180⁰)

2.  Pada trapesium samakaki, ukuran sudutsudut alasnya sama.

3. Pada trapesium sama kaki, panjang diagonal-diagonalnya sama.

4. Trapesium siku-siku mempunyai tepat dua sudut siku-siku.

Luas daerah trapesium sama dengan setengah hasil kali tinggi dan jumlah panjang sisi yang sejajar

Misal L adalah luas daerah trapesium yang mempunyai tinggi t dan panjang sisi-sisi yang sejajar a₁ dan a₂, maka

L = 1/2 × t × ( a₁ + a₂ )

Bangun Ruang SMP Kelas 7

BANGUN RUANG

        Sebuah bangun ruang, dalam konteks geometri ruang, adalah himpunan semua titik, garis, dan bidang dalam ruang berdimensi tiga yang terletak dalam bagian tertutup beserta seluruh permukaan yang membatasinya.

Terdapat dua bentuk bangun ruang, yaitu bangun ruang sisi datar dan bangun ruang sisi lengkung.

A. Bangun ruang sisi datar

Bangun ruang dengan sisi datar adalah bangun ruang yang dibatasi oleh bidang datar.

 1. Kubus

        Kubus merupakan bangun ruang yang dibatasi oleh enam buah persegi yang kongruen (Kongruen ialah suatu bangun yang memiliki bentuk dan ukuran yang sama). Gambar di atas  memperlihatkan bahwa kubus memiliki 8 titiksudut dan 12 rusuk dengan panjang yang sama. Contoh yang paling sederhana dari kubus adalah dadu.

2. Balok

        Balok mirip dengan kubus, yaitu memiliki 8 titiksudut dan 12 rusuk. Balok dibatasi oleh tiga pasang persegipanjang yang kongruen dan masingmasing pasangan yang kongruen ini terletak sejajar. Contoh balok dalam kehidupan sehari-hari diantaranya adalah ruang kelas, kotak kemasan karton, dan balok kayu.

a. Jaring-jaring

Jika sebuah polyhedron (bangun ruang sisi datar) dipotong pada beberapa rusuknya dan dapat dibuka untuk diletakkan pada suatu bidang datar sehingga membentuk susunan yang saling terhubung, maka susunan yang terbentuk disebut sebagai jaring-jaring.

b. Luas Permukaan

- Kubus

Kubus, dimana semua panjang rusuknya sama (p = l = t = a), diperoleh luas permukaan kubus = 6a²

- Balok

Perhatikan gambar di atas Jika panjang rusuk balok adalah p, lebar l , dan tinggi t, maka luas permukaan balok = 2pl + 2pt + 2lt = 2(pl + pt + lt). 

c. Volume

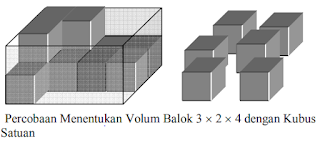
        Jika pada geometri datar luas suatu bangun dinyatakan sebagai banyaknya satuan luas yang dapat menutup bangun datar, maka dalam geometri ruang volum atau isi bangun ruang dinyatakan sebagai banyaknya satuan isi yang dapat mengisi bangun ruang tersebut. Volum diukur dalam satuan kubik, seperti centimeter kubik (cm³), inchi kubik (in³), atau meter kubik (m³). Satu cm³ menyatakan volum kubus dengan panjang rusuk 1 cm. Satuan lain untuk volum diantaranya adalah liter (1000 cc), gallon, barel, dan sebagainya.

Melalui proses percobaan dengan mengisi kubus satuan ke balok dalam berbagai ukuran, secara umum volum balok dengan panjang   p, lebar l, dan tinggi t dapat dinyatakan sebagai

volum balok = p ´ l ´ t

Mengingat bahwa alas balok (A) berbentuk persegipanjang dengan luas A = p ´ l, maka volum balok dapat juga dinyatakan sebagai hasil kali luas alas dengan tinggi balok.

volum balok = A´ t

Oleh karena pada kubus dengan panjang rusuk a berlaku p = l = t = a, maka volum kubus dapat dinyatakan sebagai: volume kubus = a³

3. PRISMA

Prisma adalah bangun ruang yang dibatasi oleh dua bidang segi-n yang sejajar dan kongruen, serta bidang-bidang tegak yang menghubungkan bidang segi-n tersebut.

 

Dua segi-n ini disebut alas dan tutup, sedangkan permukaan prismatik di antara keduanya disebut sisi prisma. Tinggi prisma dinyatakan sebagai jarak antara bidang alas dan bidang tutup. Rusuk-rusuk yang terletak pada sisi prisma dinamakan rusuk sisi dan rusuk yang terletak bagian alas dinamakan sebagai rusuk alas. Jarak antara bidang alas dan tutup merupakan tinggi prisma. Apabila rusuk-rusuk sisi prisma tegak lurus terhadap alas, maka dinamakan sebagai prisma tegak, dan selain yang demikian, dinamakan sebagai prisma miring

Perhatikan bahwa balok juga termasuk prisma, yaitu prisma yang alasnya berbentuk persegipanjang! Demikian juga dengan kubus. Prisma diberi nama menurut bentuk alasnya. Contoh: prisma segitiga samasisi, prisma segienam beraturan, dan prisma segilima beraturan

a. Volume prisma segitiga siku-siku

Volum prisma segitiga siku-siku dapat dicari dengan membuat dua buah prisma segitiga siku-siku yang kongruen sehingga dapat dibentuk menjadi sebuah balok.

Misalkan V merupakan volum prisma segitiga siku-siku dengan luas alas A. Jika dua buah prisma segitiga siku-siku digabungkan menurut sisi miring alas maka akan terbentuk sebuah balok dengan luas alas 2 ´ A.

 

2 ´ V = volum balok

= luas alas ´ tinggi

= (A + A) ´ t

= 2A ´ t

Sehingga diperoleh

V          = A ´ t,

atau volum prisma segitiga siku-siku = luas alas x tinggi.

b. Volume prisma segitiga sembarang

Misalkan volume prisma ABC.DEF, APC.DQF, dan CPB.FQE berturut- turut dinyatakan sebagai V_ABC.DEF, V_APC.DQF dan V_CPB.FQE maka

VABC.DEF             = VAPC.DQF + VCPB.FQE

= luas ∆APC ´ t + luas ∆PCB ´ t

= L₁ ´ t + L₂ ´ t

= (L₁ + L₂) ´ t

= luas ∆ABC ´ tinggi

Secara umum rumus volume prisma ialah : Luas Alas x tinggi

 

c. Jaring-jaring dan Luas Permukaan Prisma

Berikut ini merupakan contoh jaring-jaring prisma segitiga dan segienam beraturan.

Melalui ilustrasi dua jaring-jaring prisma di atas, maka luas permukaan prisma dapat ditentukan dengan jalan menjumlahkan luas sisi prisma, luas tutup, dan luas alas.

luas permukaan prisma = luas sisi prisma + luas alas + luas tutup

luas permukaan prisma = (keliling alas × tinggi prisma) + 2 × luas alas

 

4. LIMAS

Limas adalah suatu bangun ruang yang dibatasi oleh sebuah segi-n dan segitiga-segitiga yang mempunyai titik puncak persekutuan di luar bidang segi-n itu.

Segi-n dari limas ini dinamakan sebagai alas, titik Z disebut puncak limas, dan permukaan piramidal yang menjadi bagian dari limas dinamakan sisi limas. Ruas garis yang menghubungkan puncak dengan sudut-sudut alas dinamakan rusuk sisi, untuk membedakan dengan rusuk alas. Tinggi limas dinyatakan sebagai jarak terpendek antara titik puncak dengan bidang alas. Limas segi-n memiliki n buah rusuk sisi yang berbentuk segitiga, n buah rusuk sisi, dan n buah rusuk alas, sehingga banyak rusuk limas segi-n adalah 2n.

Jika alas limas berbentuk segi-n beraturan, maka dinamakan sebagai limas segi-n beraturan. Limas segi-n beraturan dikatakan sebagai limas tegak jika titik kaki garis tingginya terletak pada pusat alasnya. Limas segi-n beraturan memiliki n sisi berbentuk segitiga samakaki.

a. Volume Limas Segi-n

Sebagai contoh perhatikan limas segilima Z.ABCDE pada gambar di atas Misalkan V menyatakan volum limas Z.ABCDE, V₁ menyatakan volum limas Z.ABE, V₂ menyatakan volum limas Z.BEC, V₃ menyatakan volum limas Z.ECD, dan t menyatakan tinggi limas, maka:

Secara umum limas segi-n selalu dapat dipecah menjadi limas-limas segitiga yang mempunyai tinggi sama dengan tinggi limas yang diberikan. Dengan demikian, volum prisma segi-n dengan tinggi t adalah

Volume limas = 

a.       Jaring-jaring dan Luas Permukaan Limas

Berikut ini merupakan contoh jaring-jaring limas segitiga dan segilima beraturan.

Melalui ilustrasi dua jaring-jaring limas di atas, luas permukaan limas dapat ditentukan dengan menjumlahkan luas sisi limas dan alasnya.

luas permukaan limas = luas seluruh sisi limas + luas alas

B. Bangun Ruang Sisi Lengkung

Yang termasuk dalam kategori bangun ruang sisi lengkung adalah bangun ruang yang paling tidak memiliki satu sisi lengkung. Beberapa bangun ruang sisi lengkung mungkin sulit didefinisikan secara tepat, namun bangun ruang tersebut dapat diidentifikasi melalui sifat-sifat atau proses terbentuknya. Contoh bangun ruang sisi lengkung: kerucut, tabung, dan bola.

Modul Bangun Ruang Lengkap : Geometri Ruang SMP Kemdikbud